Конус. Зрізаний конус.

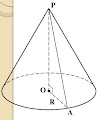
Тестові завдання для теми: "Конус. Зрізаний конус."

1. У конусі радіус і висота відповідно дорівнюють 6 см і 8 см. Встановіть відповідність між елементами конуса та їх числовими значеннями:

1. Твірна конуса	1.  72 π см2
2. Площу осьового перерізу	2.  36 π см2
3. Площа основи конуса	3.  5 см2
4. Відстань від центра основи до       середини твірної	4.  10 см 5.  48 см2

2. Через твірні конуса проведено площину. Довжина хорди СD 10 см. Твірна і висота конуса відповідно дорівнюють 13 см і 5 см.

    Встановіть відповідність між елементами конуса та їх числовими значеннями:

1. Радіус основи конуса	1.  30 см2
2. Відстань від центра основи до хорди     CD.	2.  6 см
3. Площа ∆ QOC	3.  12 см
4. Площа перерізу конуса	4.  √ 119 см
	5.  60 см2

3. Встановити відповідність між геометричними фігурами та їх площами.

                           

1. ∆ SOB	1.  S = ½ ∙ SO ∙ OA
2. S осн.конуса	2.  S = ½ ∙ AB ∙ SO
3. ∆ SOА	3.  S = 2 π ∙ OA2
4. ∆ SBА	4.  S = ½ ∙ OВ ∙ SO
	5.  S = π ∙ OA2

4. Встановити відповідність між елементами конуса та їх довжинами, якщо SO = H;   OSA = β,     ASB = α, OR ┴AB

1. OA	1.
2. SB	2.
3. AB	3.  H tg β
4. OR	4.
	5.

5. Якщо радіус основи конуса дорівнює R, твірна е, то висота конуса дорівнює :

а),  б),   в),   г)

6. Якщо радіуси основ зрізаного конуса дорівнюють 4 і 1 см, а твірна 5 см, то висота конуса дорівнює:

а) 4 см,  б) 5 см,  в) 6 см,  г) 7 см.

7. Якщо радіус основи конуса дорівнює R, висота – Н, то твірна дорівнює:

а),  б),   в),   г)

8. Якщо через дві твірні конуса, кут між якими дорівнює α, проведено переріз, а радіус основи конуса дорівнює R, твірна утворює з площиною основи кут β, то площа перерізу дорівнює:

а),    б),    в),     г)

9. Переріз конуса, що проходить через вісь – коло:

□  так

□  ні

10. Відрізки, що сполучають вершину конуса з точками основи – твірні:

□  так

□  ні

11. Переріз конуса площиною, що проходить через його вершину є різносторонній трикутник:

□  так

□  ні

12. Твірні конуса – рівні:

□  так

□  ні